Thermodynamics
Thermodynamics is the field of study that deals with the generation, use, and transfer of energy. Energy comes in many forms:
- Potential
- Kinetic
- Internal
- Chemical
- Nuclear
- Electrical
Common forms of energy transfer in the field of thermodynamics:
- Heat: Energy transfer due to a temperature difference
- Work: Energy transfer due to a force acting over a displacement
Fluid Properties
Fluids include two states of matter, gases and liquids, and can be a mixture of both. There are a few commonly used properties that will define the state of a fluid. Typically knowing two of these properties should allow you to look up or calculate the third. The most common properties are:
- Specific Volume/Density
- Pressure
- Temperature
Specific Volume/Density
Specific volume and density are measures of average mass distribution throughout a substance. Specific volume is defined as:
\nu=\dfrac{V}{m}
Density is the reciprocal of specific volume:
\rho=\dfrac{m}{V}=\dfrac{1}{\nu}
- V is the volume of given fluid
- m is the mass of given fluid.
Question
A fluid has a density of 1500 \text{kg}/\text{m}^3, and occupies a space of 2 \text{m}^3. What is the mass of the fluid?
Step 1. Given Values
\rho=1500 \text{kg}/\text{m}^3
V=2 \text{m}^3
Step 2. Governing Equations:
\rho=\dfrac{m}{V}
m=\rho V
Step 3. Solve:
m=2(1500)
m=3000 \text{kg}[/katex]
Question
A fluid has a mass of 0.15 \text{kg}, and occupies a space of 25 \text{L}. What is the specific volume of the fluid?
Step 1. Given Values:
m=0.15 \text{kg}
V=25 \text{L}=0.025 \text{m}^3
Step 2. Governing Equations:
\nu=\dfrac{V}{m}
Step 3. Solve:
\nu=\dfrac{0.025}{0.15}
\nu=0.16667 \text{m}^3/\text{kg}
Pressure
Pressure is the result of a force acting upon a given area. Therefore pressure can be described by:
P=\dfrac{F}{A}
- F is the force acting upon the area.
- A is the area that the force acts upon.
Piston-cylinders are a common component for many mechanical systems. Cylinders are also an excellent case study for applying the concept of pressure.
The piston can move up and down the cylinder. The surface pressure of the fluid(s) in contact with the cylinder will determine whether or not it will be moving. The only other force acting upon the piston is its mass, wall friction is being neglected.
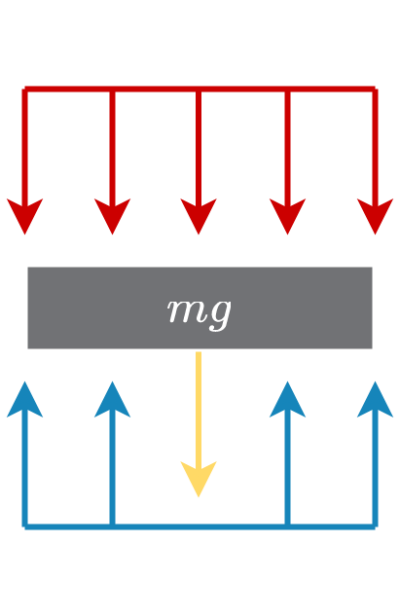
The resulting force balance will be:
P_fA=P_0A+mg
- P_f is the pressure of the fluid
- P_0 is atmospheric pressure
- A is the piston corss-sectional area
- m is the piston mass
The fluid pressure at a given depth of fluid, z, is given by the following equation:
P_f=P_0+\rho_fzg
For a series of n different fluids:
P_f=P_0+\sum_0^n\rho_iz_ig
Question
A piston-cylinder has a cross-sectional area of 0.25 \text{m}^2 and a mass of 5 \text{kg}. The piston is floating on top of a fluid and is exposed to an atmospheric pressure of 100 kPa.
Step 1. Given Values:
A=0.25 \text{m}^2
m=400 \text{kg}
P_0=100 kPa=100000 Pa
Step 2. Force Balance (Draw Free Body Diagram):
P_f A=mg+P_0A
P_f=\dfrac{mg}{A}+P_0
Step 3. Solve:
P_f=\dfrac{400(9.81)}{0.25}+100000
P_f=115696 \text{Pa}=115.696 \text{kPa}
Question
A water has a density of 1000 \text{kg}/\text{m}^3. A piston cylinder is set up in the arrangement below and remains static. The piston has a mass of 300 \text{kg} and cross-sectional area of 0.3 \text{m}^2. The height of the water on the left cylinder is h_1=2 \text{m}. What is the height of the water, h_2 in the right cylinder. Both cylinders are exposed to an atmospheric pressure of 100 kPa.

Step 1. Given Values:
\rho=1000 \text{kg}/\text{m}^3
m=300 \text{kg}
h_1=2 \text{m}
Step 2. Governing Equations:
Recognize that the pressures at the bottom of both cylinders must be equal for the system to be static.
P_{left}=P_{right}
P_0+\rho gh_1=P_0+\dfrac{mg}{A}+\rho gh_2
\rho h_1=\dfrac{m}{A}+\rho h_2
h_2=h_1-\dfrac{m}{\rho A}
Step 3. Solve:
h_2=2-\dfrac{300}{1000(0.3)}
h_2=1 \text{m}
Temperature
Temperature is a measure of average molecular kinetic energy, that is, how fast individual molecules of a substance are moving. Absolute zero (zero Kelvin) is the lowest possible temperature. No molecular motion would occur at absolute zero and so no transfer of thermal energy from the material would be possible.
Macro vs. Microscopic
The macroscopic view treats substances as continuous rather than being made of discrete parts (molecules). Macroscopic properties include pressure, temperature, and specific volume. The microscopic view takes the actions of individual molecules into account. Generally utilization of the microscopic view will require statistical analysis.
Control Mass vs. Volume
A control mass, or closed system, is a system drawn around a given mass. No mass flows in or out of the system during a process. Energy may flow in and out of the system. An example of a control mass is a piston-cylinder.
A control volume, or open system, is a system drawn around a given volume. Both mass and energy can flow through a control volume. An example of a control volume is a steam power cycle.
Some terms apply to systems:
- Insulated: Zero heat exchange (Q=0)
- Isolated: Zero work (W=0)
Processes and Cycles
Processes occur when systems change from one state to another. States define the physical characteristics of a system at a specific time. System changes are due to energy transfer between the system and its surroundings. Cycles occur when a system goes through a series of processes and ends at its original state.
A quasi-equilibrium process assumes that for any instant during the process the system is at thermodynamic equilibrium. Some common quasi-equilibrium processes are:
- Isothermal: Process occurs with a constant temperature
- Isobaric: Process occurs with a constant pressure
- Isometric: Process occurs with a constant volume
- Adiabatic: Process occurs without heat transfer
- Zero work: Process occurs without any work
Laws of Thermodynamics
- Zeroth Law: When two bodies maintain thermal equilibrium with a third body then the first two bodies must also be in thermal equilibrium
- First Law: Energy can not be created or destroyed, only transferred and transformed
- Second Law: The sum of entropies in a system must lead to an increase in overall entropy
- Third Law: As a system approaches absolute zero the entropy of the system will approach a constant value
